An updated look on squaring the circle using gganimate and R code.

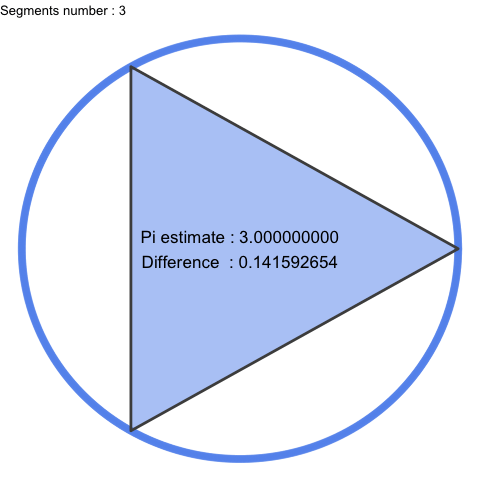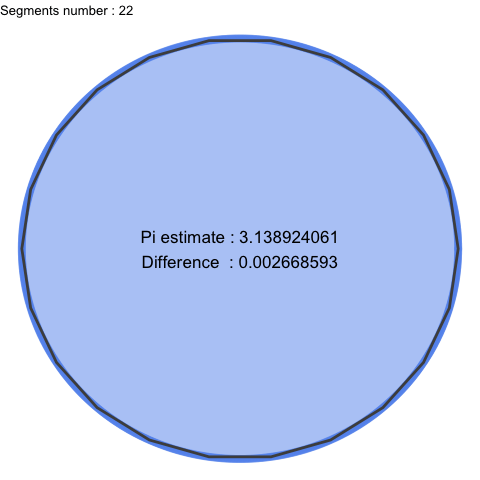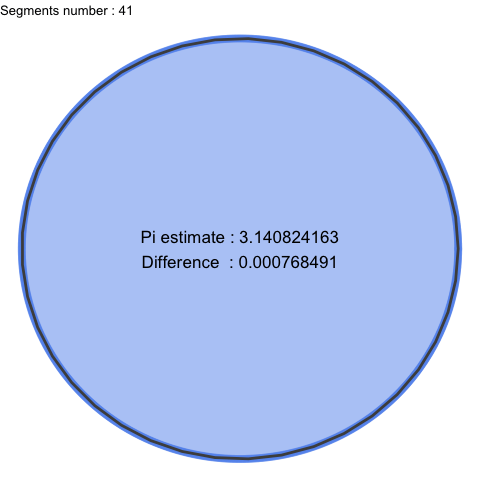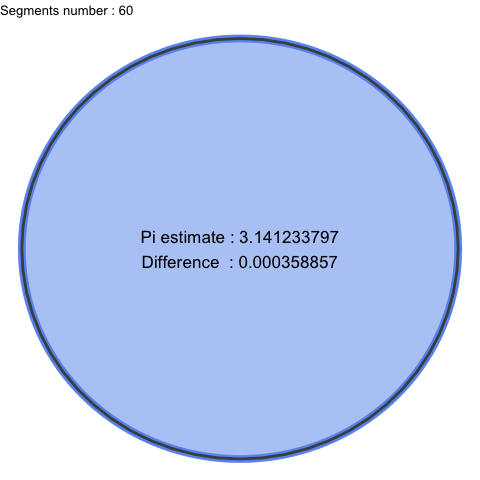
It gives a geometric and visual construction, a good and practical representation of what Pi is. As n becomes larger, segments become smaller and smaller, Pi can then be seen as perfection and we almost intuit infinity.

require(sp)
require(rgeos)
library(ggplot2)
library(dplyr, warn.conflicts = FALSE)

x <- 0.5 # center x
y <- 0.5 # center y
n <- 1000 # nr of pts
r <- 0.5 # radius


poly <- function(n){
  library(dplyr, warn.conflicts = FALSE)
  j <- n %% 2
  theta <- (2 - j):(2 * (n) + 1)
  
  u <- tibble(theta = theta, x = cos(theta * 2 * pi / n), y = sin(theta * 2 * pi / n))
  v <- SpatialPolygons(list(Polygons(list(Polygon(cbind(u$x,u$y))), "polygon")))
  v <- ggplot2::fortify(v) %>% mutate(n = n)
  
  return(list(df = u, poly = v))
}

pts <- seq(0, 2 * pi, length.out = n)
plot(sin(pts), cos(pts), type = 'l', asp = 1) # test

nmax = 60
alls <- 3:nmax %>% purrr::map(function(x)poly(x)$poly) %>% bind_rows()  %>% 
  mutate(estimate = round(sqrt(2 - 2 * cos(pi / n)) * n, 9))


circles <- bind_rows(lapply(tibble(x = cos(pts), y = sin(pts)), rep, nmax - 2 )) %>% 
  mutate(n = rep(3:nmax, each = 1000)) %>% 
  as_tibble() %>% 
  mutate(estimate = round(sqrt(2 - 2 * cos(pi / n)) * n, 9),
         estimate = paste0('Pi estimate : ', format(estimate, digits = 10), '\n', 
                           'Difference  : ', format(round(pi - estimate, 9), digits = 9)))

library(ggplot2)
library(gganimate)
p <- ggplot() +
  geom_point(data = circles, aes(x = x, y = y), col = 'cornflowerblue', lwd = 3, alpha = 0.5) + 
  theme_void() + 
  geom_polygon(data = alls, aes(x = long, y = lat, group = n), col = 'grey30', lwd = 1.3, fill = 'cornflowerblue', alpha = 0.5) + 
  geom_text(data = distinct(circles, n, .keep_all = TRUE), aes(x = 0, y = 0, label = estimate), size = 6) + 
  labs(title = 'Segments number : {frame_time}') + 
  transition_time(n)

p

More information and some links of inspirations are here in the code:

https://github.com/Guillaumepressiat/under_pi

And I have made a really long gif here:

https://raw.githubusercontent.com/GuillaumePressiat/under_pi/master/under_pi_patient_geek.gif